Simulacra And Selection

How many sets of 5 can you make from 10,000 distinct items? Recall that chapter about permutations and combinations…

…that’s right, it’s “n choose k.” The answer is too big to write out here, making this a hard problem to contemplate. Additionally, many subsets are not even plausible or coherent. Yet, due to the size and sparsity of the problem, most possible subsets will never be observed, whether they are plausible or not. We face this challenge in choosing items to feature, recommending complementary items, market basket analysis, and so on. While difficult to tackle, these problems also offer a lot of opportunity. In this post, we discuss how modeling a subset selection problem has enabled our stylists to spend less time browsing and more time curating, deepening the interaction between human and algorithm.

Styling at Stitch Fix

Modern retailers aid and influence customer decisions, using techniques like recommender systems and market basket analysis to deliver personalized and contextual item suggestions. While such methods typically just augment a traditional browsing experience, Stitch Fix goes a step further by exclusively delivering curated selections of items, via algorithmically-assisted stylist recommendations¹.

For most of the history of Stitch Fix, stylists have worked with a styling platform that functions in a fairly straightforward way. For simplicity and concreteness, imagine an e-commerce platform with various filters, wherein stylists are able to browse for clothing items and add them to a cart. The role of our styling algorithm in this system is to rank the items based on information the client provides us, and the role of the stylist is to select an assortment of items that a client will love.

I’m going to gloss over all the details of the styling algorithm except for one important and nuanced point: it is trained to estimate the probability that a particular client will like a given item if a stylist decides to send it. This is a natural and useful framing: we observe what happens to items that stylists select, but not the counterfactual for items they don’t select. However, this selection bias comes with some occasionally perplexing caveats. One observation of long-standing Stitch Fix lore is the “shorts in winter” problem: the styling algorithm tends to assign a high score to shorts during the dead of winter. Do we somehow think that everyone wants to stock up on shorts despite the chilly weather? Of course not: this only means that shorts are likely to be successful if a stylist chooses to send them, which they won’t do without a very good reason—e.g., a client requesting them for a tropical cruise. This is an amusing example but the problem is broader: stylists need to spend a decent fraction of their time browsing through items that, for one reason or another, are clearly a poor match.

At this point the inspired data scientist might ask: why not attempt to correct for selection bias and estimate the unconditional client response instead? Even though the quantity is not observed directly, techniques from social science like the Heckman correction provide a path for estimating it. While this is theoretically elegant, our team’s efforts to incorporate selection corrections have never delivered the outcomes we thought should be possible. Why not? It’s hard to know for sure, but let’s consider the parable of the beautiful ill-fitting blouse.

A Parable

This beautiful blouse is almost perfect. It is trendy yet democratic, fresh but familiar. It has just the right pop of color to catch the eye, but subtle enough to not throw an outfit off-balance. It can be dressed up or down. It has only one flaw: the fit is very particular. Sure it looks great in lay-downs, and even happens to work well on the model. But the model isn’t most people, and for most people our styling algorithm knows that it’s just not going to work. Tragically, a stylist who sees this blouse can hardly help but send it. The blouse is a siren call, and like Odysseus tied to the mast, only the restraint of the algorithm can prevent the stylist from succumbing to its song. Modeling out the selection bias amounts to a loosening of the restraints, as items that are less likely to be selected (but better fitting) will be ranked below the siren blouse. Without removing selection bias, the better fitting but less visually appealing selections will be ranked higher, one will be more likely to be chosen, and everyone will be better off.

What a tragic story. Surely there is no hope for modeling selection, it will only throw us into the waves. Or perhaps not: we’ve demonstrated that selection is not a useful correction to conditional purchasing, but perhaps conditional purchasing can be a useful correction to selection. In a sense, this is what we are doing already! By using conditional purchasing to rank items, we are nudging stylist selection in the direction of client preferences. This simple approach has taken us a long way, but let’s imagine going a step further. Suppose we can model exactly what items a stylist will select for a given client. We could then take this selection and nudge it further in the direction of client preferences. To the extent that our models are accurate, this nudge will lead to a corresponding increase in client satisfaction².

Obviously, we can’t know exactly what a stylist will select for a given client, nor are we interested in replacing our stylists with robots. However, we don’t need perfect simulacra. If we can build a “good enough” model of stylist selection that takes into account the many and varied interactions a stylist considers when assembling a set of items, we can present stylists with a pre-filled set of selections (with our nudge included), and ask them to edit it. This transforms our stylists from browsers to curators, and has other positive knock-on effects, such as improved efficiency. Our new styling platform is built to accommodate this transformation, making contextual set selection an intuitive tool for stylists.

Contextual Set Selection

This contextual set selection problem has much in common with other recommendation system problems, like personalized video or e-commerce recommendations. However, unlike general recommendation problems, set coherence is particularly important. This is intuitive: if a stylist has already selected a pair of jeans, they are less likely to want a second pair of jeans and more likely to want a blouse that pairs well with the jeans they already picked out. It is also pervasive: humans are so good at taking in a holistic gestalt that we hardly even notice the relationships we are considering to do it. To successfully model human selection, we must account for these interactions, and modify our recommendations appropriately. Similar constraints exist in other areas, particularly market basket analysis: a supermarket customer buying bread might also want butter, while an online shopper looking at printers might also want ink.

Our approach to set selection is framed by two major challenges. The primary challenge is the fact that the space of possible sets is incredibly large and sparse compared to the observed sets. Unlike most recommendation problems, any particular set is extremely unlikely to ever be observed, and any set that is observed will probably never be observed again. Thus, any proposed model will need to contend with this intrinsic sparsity.

The second challenge of contextual set selection is that sets are unordered. This is a challenge mostly because it means we cannot directly leverage well-studied sequence problems such as natural language modeling, which are otherwise some of the closest analogs to our problem. However, this is also something of a mixed blessing: while we can’t take advantage of adjacency effects to simplify item-item interactions, we also don’t need to worry about respecting properties like transitions or grammar that are endemic to ordered sequences.

Keeping these challenges in mind, we make the following modeling decisions:

• Likelihood-based objective: we will model set selection probabilities by maximizing the likelihood of observed sets
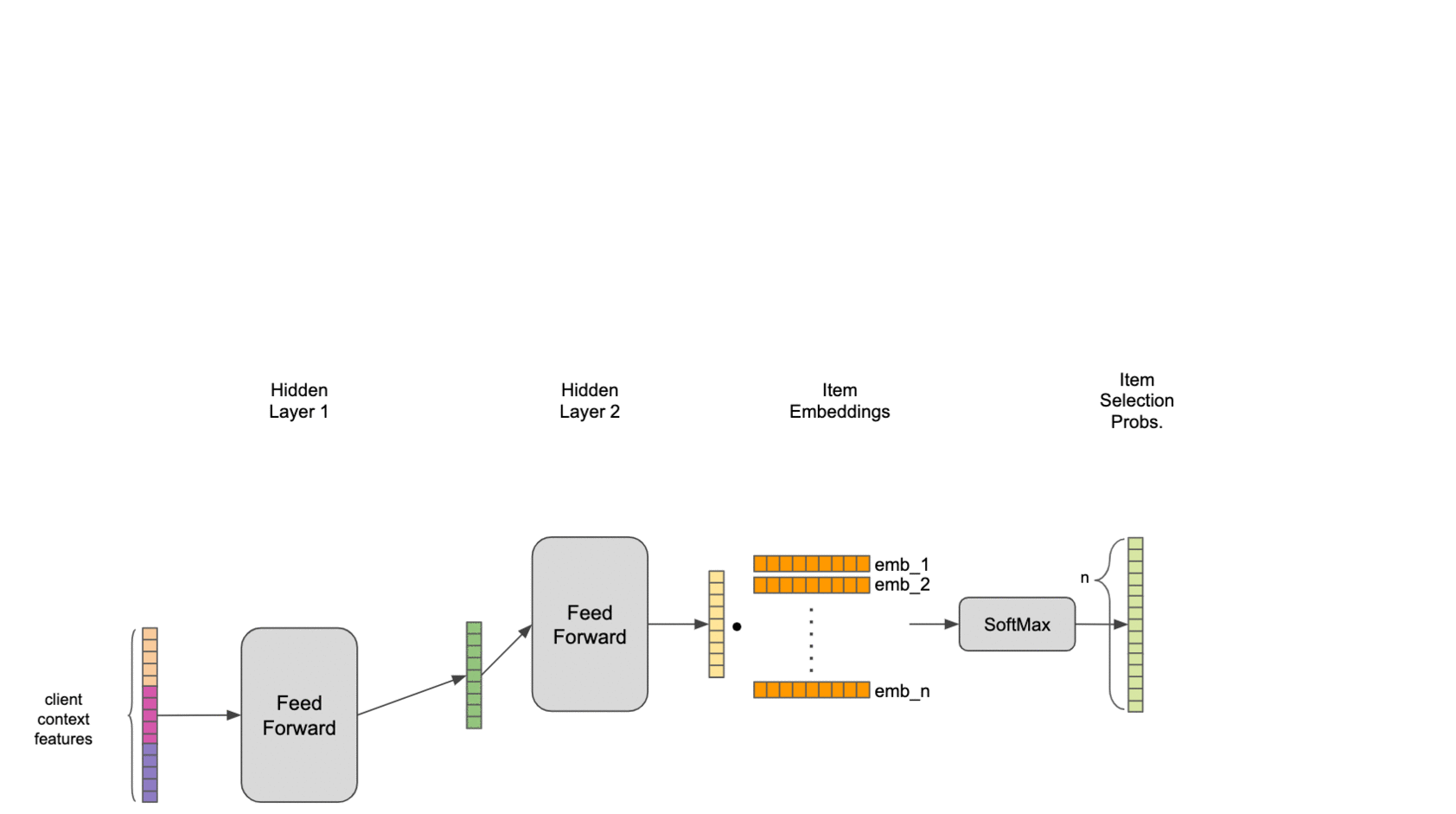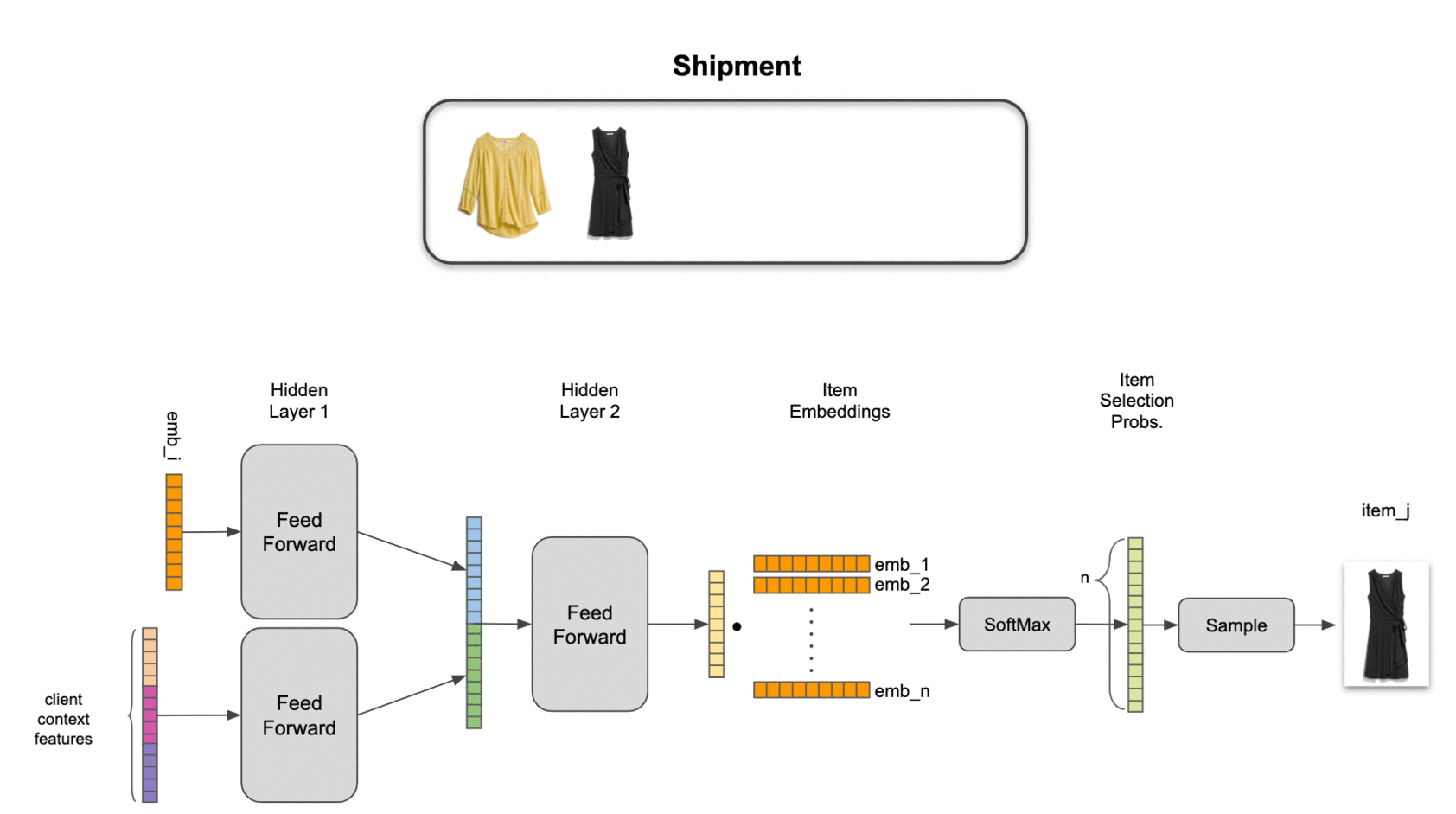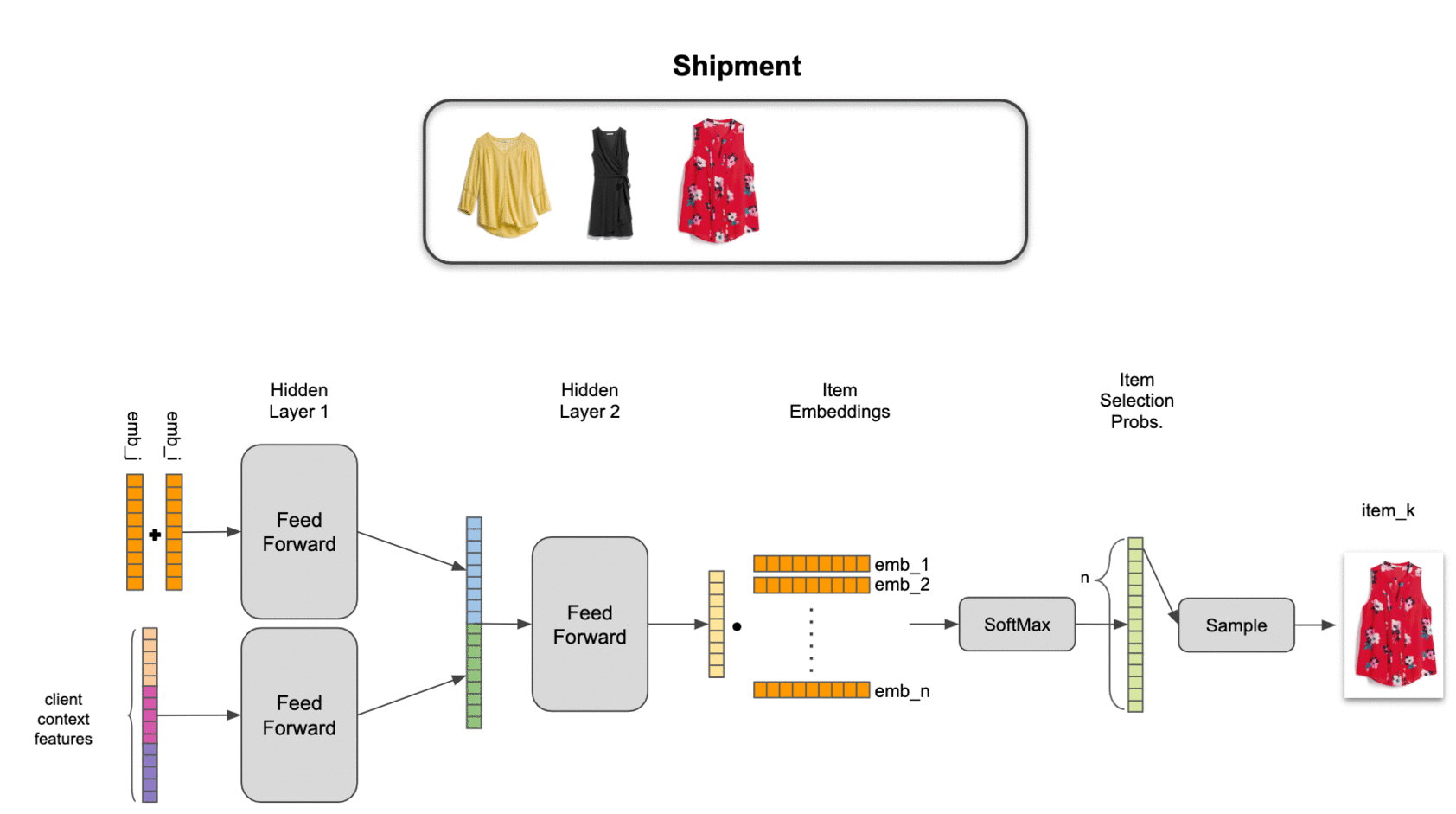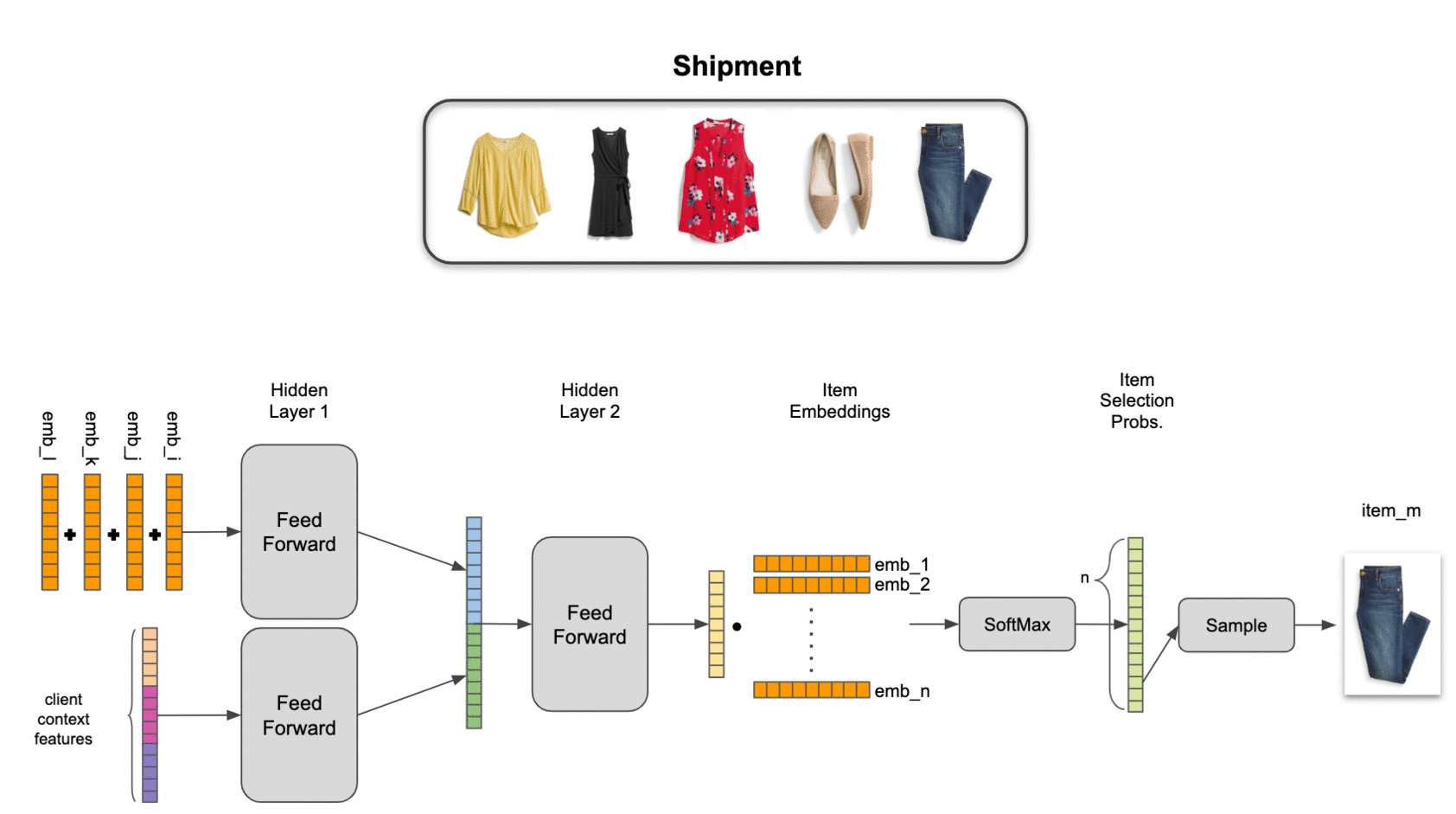
• Conditional probability: we will decompose set selection probabilities as the product of conditional probabilities, ie, \(P(ABC) = P(A) P(B \vert A) P(C \vert AB)\)
• Latent item representations: we will learn dense embedding vectors for the items in our inventory
• Pooled set representations: we will define an aggregation to combine a set of items in a fixed-dimensional vector representation

Let’s look at the motivation behind these decisions in some detail. First, the choice of objective function sets the direction for the rest of the modelling work. We want to be able to sample from conditional item probabilities, so maximizing likelihood is a natural choice. We also considered adversarial distribution approximation methods, but these tend to be less effective on discrete data and less straightforward to interpret. Additionally, we have a wealth of data of observed sets (styled shipments), providing ideal training data for a maximum likelihood estimate. Another framework we rejected is determinantal point processes, which are well-suited to set diversity, but less so to set cohesion.

The conditional probability decomposition is an essential component of making the set estimation problem tractable. By considering only a single item at a time, we avoid the combinatorial explosion of the full joint selection space, at the cost of needing to model conditional context of varying size. This also introduces a new problem: while the joint probability is symmetric:

the estimated decomposition may not be:

However this is not a major concern in practice. We also mitigate any order dependence by shuffling the order of the sets during model training.

Latent item representations allow us to further reduce the number of free parameters in the model. Even with the conditional probability simplification, our inventory is too large to learn interactions directly. Learning a latent representation for each item allows us to model interactions between low-dimensional dense vectors rather than high-dimensional sparse vectors.

An implication of conditional probability decomposition and latent item representation is that we need to use a pooled item set representation to combine context from multiple items. This allows us to estimate probabilities for an item conditional on 4 other items just as easily as for an item conditional on 1 other item. We’ve explored several pooling mechanisms, including attention, but find a simple sum of latent item representations to work best in practice on our data.

To tie it all together, we combine the pooled set representation and contextual features with two neural network hidden layers, providing a nonlinear transformation to an output layer with the same dimensionality as the item embeddings. Final estimated selection probabilities are taken as the softmax of the output layer with the items in inventory.

We find that this model significantly outperforms item-independent models, as well as traditional association-rule-based market basket analysis. Even more importantly, it passes the practical test of adding value for our stylists: by training our algorithms to act a little more human, we’ve been able to help make our stylists more efficient while also improving their ability to help our clients discover clothing they love.

Footnotes

[1]↩ Personalizing Beyond the Point of No Return

[2]↩ Why nudge rather than shove? We have to stay locally valid to selection for our client preference model to be valid, so there’s a limit to how far we can push. Exactly how far is an empirical question.