Data-Driven Fashion Design

A core methodology at Stitch Fix is blending recommendations from machines with judgments of expert humans. Our machines produce recommendations via algorithms operating over structured data, while our human stylists curate and modify these recommendations on the basis of unstructured data and knowledge that isn’t yet reflected in our dataset (e.g., new fashion trends). This helps us choose the best 5 items to offer each client in each fix. The success of this strategy within our styling organization prompts consideration of how machines and humans might be brought together in the realm of fashion design. In this post we describe one implementation of such a system. In particular, we explore how the system could be implemented with respect to a target client segment and season.

Fashion design is normally achieved by a qualitative process focused on stylistic intent and inspiration. In contrast, our team conceptualizes the design process as an algorithm searching for desirable regions (for example, points that yield maximal positive responses from our clients) within the space of possible blouses. Put another way, designing a new blouse can be thought of as searching a space with dimensions that correspond to attributes of a blouse like color, print, material fabrication, chest diameter or type of neckline. However, because this space is sparsely and non-uniformly populated with observations – that is, because Stitch Fix has collected empricial data on only a fraction of all possible blouses that will ever be made – it can be challenging to search using methods like exhaustive search or exact optimization (e.g., linear programing).

Instead, we draw inspiration from the field of genetic algorithms, which has been shown to achieve efficient search across a variety of similar problems. The proposed design system can be shaped to mimic the processes that underlie these stochastic optimization methods. In the remainder of this blog post we describe a design system being explored at Stitch Fix that blends elements of genetic algorithm with the judgments from our expert human fashion designers.

A brief introduction to genetic algorithms

Genetic algorithms are a collection of methods inspired by genetics and natural selection. Within the metaphor, each candidate solution is conceptualized as having a chromosome composed of genes, where each gene’s value is an allele. Similarly, a blouse’s chromosome is a vector of attributes corresponding to the dimensions of the search space.

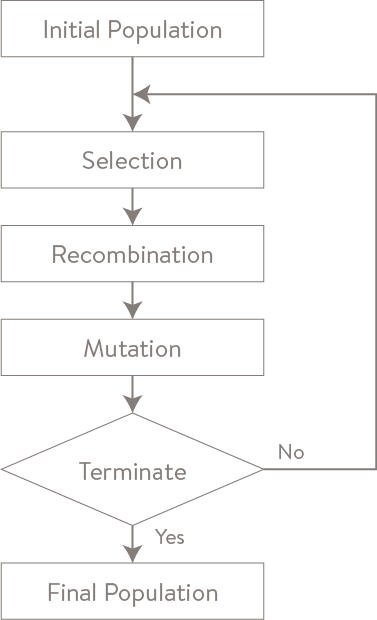
Generating a new design can then be framed as an evolutionary process searching over a population of possible blouses, through a series of generations.

Each generation passes through three stages:

1. Selection: Each individual of the current generation is evaluated for its fitness. This implies access to an explicit objective function mapping attributes to outcomes or empirical measurements of each individual in the current generation. For instance, blouses might be selected to maximize style and fit feedback. These individuals from the current generation can then enter a mating pool using not-so-natural selection procedures such as selecting the N fittest individuals, or selecting individuals with a probability proportional to their fitness (e.g., biased roulette-wheel selection).
2. Recombination: Individuals in the mating pool are bred to produce new individuals that are hopefully desirable and novel because they were created by decomposing two good parents and using the resulting elements to compose a child. There are a variety of procedures for implementing recombination. They essentially boil down to using a random mix of features from each parent versus various implementations of passage of clustered features (see k-point cross-over). An example of the latter in our system might be passing sleeve type, sleeve length, and sleeve fabric as a unit. Additionally, we can move away from a pure genetic algorithm by assessing the feature we’re passing on globally, rather than just assessing the individual. We can then propose which genes to select from each parent using this broader knowledge.
3. Mutation: Diversity and novelty are introduced into new generations by randomly changing alleles. These mutations search the vicinity of the solution space via a random walk. This vicinity can be more or less local depending on the type of mutations that are employed. For instance, the values of different alleles can be assigned proportional to the observed distribution of alleles or forced into their extremes to achieve a more aggressive search (e.g., boundary mutation). We’ve found a compromise between these to be practical – finding underrepresented regions of the feature space.

Leveraging Stitch Fix’s unique capabilities

Genetic algorithms rely on the heuristic that new and improved designs can be created through an evolutionary process. The methods used to achieve this (selection, recombination, and mutation) are typically stochastic. Randomness helps to implement search via an efficient but flexible exploration that is disproportionately in the vicinity of existing high performing individuals. However, finding interesting points in the space may require the creation of many individuals and generations. This poses a challenge for practical clothing designing because it’s relatively expensive and time consuming to create many new blouses, bring them to market, and empirically assess whether they delight our clients.

At Stitch Fix we have a resource that can be leveraged to improve the efficiency of this search: a team of expert human fashion designers whose judgments indicate promising paths through the solution space. Stitch Fix’s styling process (choosing which 5 recommended items to send each client) offers a model for how we might integrate and leverage the complementary abilities of machines and humans – machines recommend a generation of new designs which are then curated by human designers.

Generating Recommendations

Here we consider why and how machines can be used to create recommendations for each stage of the genetic algorithm:

Selection. If we are to mimic survival of the fittest then we need a method to evaluate fitness. For instance, we can assess each of our existing blouses with respect to:

where \(Y = 1\) (vs. 0) if sending this item elicited positive feedback, \(t\) is the time where the feedback was received within the temporal interval \(T\), and \(c\) are the clients in the targeted audience \(C\).

Here at Stitch Fix we have a variety of ways of assessing each existing design in our inventory. For instance, when a client checks out a fix they leave explicit feedback about each design’s Style, Fit, Size, and Price (i.e., \(Y\)). We’ve observed large temporal trends in how a design is perceived (no white after labor day!), so we may want to limit ourselves to considering feedback from within a temporal interval (i.e., \(T\)). Finally, our clients have different styles, body-shapes, sizes, and price preferences (among other things). So we must choose a target audience for each design and then calculate our measure of fitness from feedback from that type of individual (i.e., \(C\)).

These scores power selection recommendations that are supplied to our human fashion designers. Our fashion designers can implement a process akin to biased roulette-wheel selection procedure by preferentially selecting items from the top of our list of recommendations. To illustrate, this process yielded the selection of the two blouses below:

Recombination. Having selected a set of high performing blouses we can now consider how they should be recombined to form a new child. While a traditional genetic algorithm would stochastically search all combinations over many market generations, we can shortcut that process by algorithmically looking for features that have been historically preferred by our target client segment.

To achieve this, we find statistical regularities between the population of blouses’ attributes (or configurations of attributes) and client feedback. For instance, we can model the relationship between attributes of our existing blouses and client feedback via:

where \(y\) is the client feedback elicited by each send, \(\chi\) represents fixed effects of attributes (or configuration of attributes) of a blouse (i.e., its chromosome), \(\beta\) are learned coefficients for these fixed effects, \(Z\) is a design matrix of random effects that model how the effect of attributes differ by client segment and time range, \(\gamma\) are learned weights for these random effects, and \(\epsilon\) is unexplained (i.e., residual) variance. Inspection of this model provides insights into the types of blouses that are prefered by different types of clients at different points in time. These insights can be used to recommend which attribute from each parent design should be passed to the child design.

To illustrate, let’s consider the two shirts selected for recombination. These blouses have different sleeve lengths, so the recombination algorithm must propose which sleeve length to pass on to the child. Since modeling indicates short sleeves were consistently linked to higher client feedback in our target audience and time frame, the shorter sleeve was recommended to be passed onto the child during recombination. This recommendation will be judged against others by our human designers. Oversight by the designers allows for assessment of feature congruity that can be difficult in a sparse feature space.

Mutation. In biological evolution, mutations introduce diversity into new generations. This diversity creates the opportunity to find new and fitter individuals and to speciate and find new evolutionary niches. Mutations serve an analogous purpose in the design process in that they allow us to test new configurations of attributes and maintain diversity. This is critical for a company like Stitch Fix, whose goal is to serve the personalized needs of all our clients across style aesthetics, sizes, shapes, and price preferences.

First, we can build and analyze statistical models (as described in the recombination section) to identify which attributes of a design could be mutated in a promising direction. Second, we can look for regions of the design space that are under-represented in our inventory relative to observed client demand. We can operationalize this as,

where Stock is a count of items in our inventory, Send is a count of items that are presented to clients, \(a\) is an attribute of a design within chromosome \(A\), \(t\) is the time when feedback was received within the temporal interval \(T\), and \(c\) are the clients in the targeted audience \(C\). This identifies types of blouses that our stylists disproportionately send relative to our buying and form one basis for mutation recommendations.

To illustrate, statistical modeling might find that blouses with graphic prints are receiving very high feedback in our target time frame and client segment. Moreover, an analysis of inventory shipments might flag coral as a blouse color whose shipment volume far outpaces its stock volume. These opportunities would then be passed as recommendations to our human designers.

At the end of the day, this methodology allows for a range of selection-recombination-mutation proposals to be offered to our designers. Expert human judgment then provides the final word on what the next generation of styles will be!